Space_Sound is a study on the work of composer and architect Iannis Xenakis.
Iannis Xenakis used extensively computation and mathematics in order to create music. The initiative for this project was that while Iannis Xenakis is widely acclaimed and studied as an innovator in avant guard music, his work is not extensively examined in relation to architecture, and when that is done the focus is always on his architectural designs and mostly on the Philips Pavilion. However, Xenakis in his writings was always underlining that his methods in composition are not only applicable to music, but also to the visual arts and most notably to architecture.
Xenakis’ musical scores are composed in such a way that they have an underlying spatial dimension. His scores and diagrams for his compositions share very little resemblance to conventional musical sheets, while they could be undoubtedly “read” as spatial diagrams and architectural blueprints.
He was one of the first researchers to use computers in his musical/mathematical explorations. With a delay of some decades, the use of the computer in composition reached also the field of architecture and eventually led to a more constant, or more obvious, impact of mathematics to architecture. The architectural avant guard today has to deal with, up to a certain extent, with mathematical or computational processes like cellular automata, L-systems, stochastic process and boolean algebra, all methods employed earlier by Xenakis in his work.
Having the above in mind, Xenakis’ work could prove itself extremely helpful in relation to the questions that computation is posing to architecture today. More specifically, Xenakis’ work could provide insights for architectural practice in relation to the computers in two ways:
a. First in a theoretical level. Xenakis provides a very extensive philosophical and theoretical background for his work through his writings, which seems possible to be used also in relation to architecture today.
b. Secondly in a design oriented level. Iannis Xenakis started to use mathematics and computers as his tools for composition in the beginning of the 1960’s and continued this research until the end of his life. Therefore his work has to offer a great variety of methods, techniques and processes for the musical composition. Given the fact that Iannis Xenakis’ way of working with music was based on ‘spatial’ techniques and visualization of his ideas through drawing, a study of his projects could offer precious insight for architectural design. In addition to that, the introduction of those spatial qualities in Xenakis’ research that focuses on sound, arises questions on the relation between space and sound and how the one discipline can offer resources to the other.
So, space_sound consists mainly of visual representations of several methods that Xenakis employed in his work. Through scripting, concepts and mathematical ideas like boolean algebra, alleatory distribution of points on a plane, brownian motion, cellular automata etc. are used in order to create small animations that are trying to explore the spatial or architectural qualities that those concepts can activate.
example 01: Brownian motion
Brownian motion is a mathematical model used in order to describe the movement of particles inside fluids. Although the motion of the particles is described from various ‘brownian equations’ it can not be predicted. Therefore Brownian motion can be used in order to produce randomness.
Xenakis is employing Brownian motion in N’Schima in the context of stochastic process that he constantly applies in his compositions as the means to create randomness. In N’Schima Brownian motion is defining the glissandi that the various instruments are following.
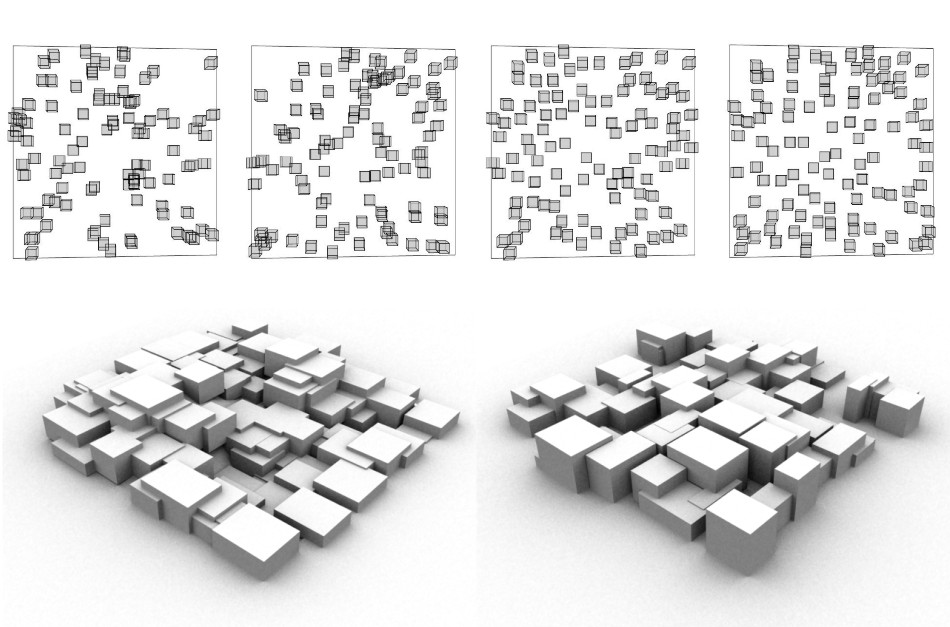
example 02: Aleatory distribution of points
Aleatory distribution of points on a plane is a stochastic process, that is a process that is characterized by randomness, where a specific number of points are distributed on a plane in a way that satisfies specific rules.
A cellular automaton is a discrete model, which means that they don’t require the notion of continuity. Cellular automata have many applications in mathematics, computation and biology. A cellular automaton consists of a grid where each cell may have two states, empty of full (0 or 1) and a specific set of rules that defines the way that the state of the cells is changing over time. After the rules are applied to all the cell of the grid a new generation is created. Those rules are always in relation to the neighbor cells of each cell. That is the state of each cell in generation n is defined by the state of its neighbor cells in generation n-1. One of the most famous set of rules is Conway’s Game of Life:
1. Any live cell with fewer than two live neighbors dies, as if by loneliness.
2. Any live cell with more than three live neighbors dies, as if by overcrowding.
3. Any live cell with two or three live neighbors lives, unchanged, to the next generation.
4. Any dead cell with exactly three live neighbors comes to life.
One of the most interesting properties of the cellular automaton is that it requires no input from the user (therefore an automaton). It is a self referential process where the output of each generation is becoming the input for the next one. What is also interesting is that from a very specific and simple set of rules, when we let the automaton to evolve, we can produce very complex formations.
Xenakis used cellular automata in many of his later works, for example Ata and Horos, in order to create new harmonic progressions.
 |
 |
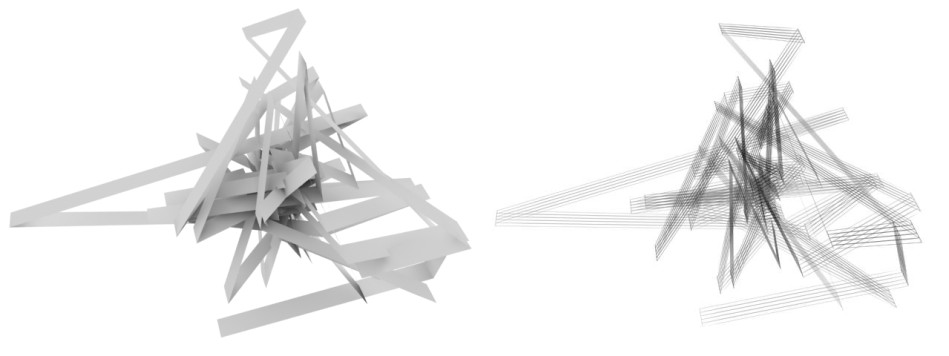
example 04: Boolean algebra
Boolean logic is a system of logical operations. Those operations are union, subtraction and intersection.
| >>info: | |
| research: | Dimitris Gourdoukis |
| date: | 2006 |
| publications: | — “Object-e Portfolio” in Portfolio Seoul: DAMDI Publishing Co., 2010. — Gourdoukis, D., Tryfonidou, K. “What comes first: the chicken or the egg? Pattern Formation Models in Biology, Music and Design.”” in Terzidis, K. (ed) Critical Digital: What Matter(s)? Boston: Harvard University Press, 2008. |